Để Biểu Diễn Số Nguyên 100 Cần Bao Nhiêu Byte – Biểu Diễn Số Nguyên Có Dấu Trong Máy Tính Theo Kiểu Nào?
Để biểu diễn số nguyên 100 cần bao nhiêu byte
Cả Byte và Bit đều là những đại lượng được sử dụng để thống kê giám sát thông tin. Cách quy đổi giữa những đại lượng này cũng tựa như như cách quy đổi giữa các đơn vị khối lượng trong toán học. Có công thức, rất giản đơn tính toán. Cụ thể:
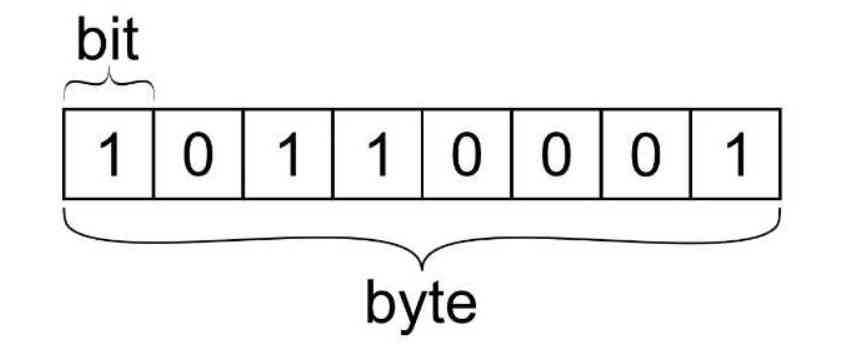
Theo quy ước quốc tế: 1 byte = 8 bit
Vậy 2 byte bằng bao nhiêu bit? Chúng ta cứ nhân lên theo công thức Số Byte x 8, được kết quả:
- 2 byte = 2 x 8 = 16 bit
- 3 byte = 3 x 8 = 24 bit
- 5 byte = 5 x 8 = 40 bit
- 100 byte = 100 x 8 = 800 bit
- 150 byte = 150 x 8 = 1200 bit
Nếu bạn rất thích biết 1 bit bằng bao nhiêu byte, chỉ việc tính ngược lại, lấy đơn vị chức năng cần tính rồi chia cho 8 là ra. Ví dụ:
- 1 bit = 1 ÷ 8 = 0,125 byte
- 10 bit = 10 ÷ 8 = 1,25 byte
- 15 bit = 15 ÷ 8 = 1,875 byte
- 100 bit = 100 ÷ 8 = 12,5 byte
- 150 bit = 150 ÷ 8 = 18,75 byte
Biểu diễn số nguyên có dấu trong máy tính theo kiểu nào?
Về cơ bản, phép AND cho kết quả là một khi và chỉ khi cả hai số hạng là 1. Nếu coi 0 là sai và một là đúng thì có thể hiểu phép AND là “A AND B đúng khi cả A và B đều đúng”.
Trong C++ có 2 phép AND là & và &&.
&& xem 2 số hạng là kiểu bool (đúng/sai), còn & thực hiện tính toántrên từng bit của 2 số hạng:
110010 (50) & 011010 (26) ------ 010010 (18)
Như vậy ta có 50 & 26 = 16.
Đối với số âm, vì trên máy tính màn biểu diễn số âm bằng kiểu bù 2 nên kết quả sẽ khác số dương:
11111110 (-2) & 00000111 (7) -------- 00000110 (6)
Như vậy ta có -2 & 7 = 6.
Giới thiệu bảng chân trị
Bảng chân trị cho phép định nghĩa những phép toán logic. Bảng chân trị của phép AND là:
| A | B | A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tính MOD (số dư)
Khi cần tính số dư khi chia cho M, với M là lũy thừa của 2 ta hoàn toàn có thể thay x % M bằngx & (M-1). Ví dụ:
x % 8 => x & 7 x % 4 => x & 3 x % 2 => x & 1
Trong máy tính, AND được triển khai nhanh hơn rất nhiều so với phép MOD, ta nên dùng AND khi có thể.
Lấy giá trị của bit
Xét một bit x, ta thấy x AND 1 = x. Từ nhận xét này, hoàn toàn có thể dùng AND để lấy giátrị của bit bất kì trong một số. Ví dụ:
- Lấy giá trị bit thứ k của x:
x & (1 << k) - Lấy giá trị 4 bit sau cuối của x:
x & 15
Tắt bit tại vị trí bất kì
Tắt bit nghĩa là gán bit tại vị trí đó bằng 0. Ta thấy x & 0 = 0, nên có thểdùng AND để tắt bit.
Giả sử cần tắt bit K trong số X. Ta triển khai AND X với số MASK thỏa:
- Bit ở đoạn K bằng 0
- Tất cả những bit còn lại bằng 1
Ví dụ, để tắt bit thứ 0, dùng x & -2.
Kết hợp với phép NOT, ta hoàn toàn có thể tạo nên MASK để tắt bit tại vị trí K: X & ~(1 << K)
Tìm bit nhỏ nhất khác 0
Đây chính là thao tác cơ bản nhất của cây Fenwick.Để cho ngắn gọn ta kí hiệu “bit nhỏ nhất khác 0” của x là F(x).
F(100) = 4, 100 có màn màn biểu diễn nhị phân là1100100, bit thấp nhất khác 0 là100có giá trị là 4.F(64) = 64, lan rộng ra hơn,F(x) = xkhi x là lũy thừa của 2.F(số lẻ) = 1, do số lẻ luôn có bit thấp nhất = 1.
Công thức: F(x) = x & -x
Phép tính này tận dụng cách biểu diễn bù 2 để tính toán. Để hiểu rõ, bạn đọc nên tính tay trên giấy.
Duyệt toàn bộ những tập con
Trong những bài toán duyệt, ta thường dùng số nhị phân để trình diễn việc chọn/không chọn một phần tử.Ví dụ, số 13 có trình diễn nhị phân là 1101, nên 13 đại diện thay mặt cho một tập hợp chứa 3 số là 0, 2, 3.
Làm thế nào khi ta cần xét tất cả những tập con của 13: 1100, 1001, 0101, 0001,…?
Việc này được triển khai nhanh bằng phép AND như sau:
#include <bitset> #include <iostream> using namespace std; int main() { int x = 13; for (int k = x; k > 0; k = (k-1) & x) { cout << bitset<4>(k) << '\n'; } }
Đoạn code ở trên dùng std::bitset để in ra màn biểu diễn nhị phân của k.Có một điều lạ là cả printf và cout đều không hỗ trợ việc in ra biểu diễn nhị phân của số.
Áo Bape Real Giá Bao Nhiêu – Áo Bape Cá Mập
Xin Cấp Điện Sinh Hoạt Hết Bao Nhiêu Tiền – Thủ Tục Xin Cấp Điện Sinh Hoạt
Vỏ Bình Ga Bao Nhiêu Kg – Bình Gas Lớn Bao Nhiêu Tiền
Vách Ngăn Cnc Giá Bao Nhiêu M2 – Báo Giá Vách Cnc Sắt
Vàng 97 Giá Bao Nhiêu – Giá Vàng 97 Hôm Nay Tại Quảng Nam
Utrogestan 200Mg Giá Bao Nhiêu – Utrogestan 200Mg Uống Hay Đặt Tốt Hơn
Tích 10 Số Tự Nhiên Đầu Tiên Bằng Bao Nhiêu – Số Tự Nhiên Lớn Hơn 1 Và Chỉ Có 2 Ước Là 1 Và Chính Nó Đó Gọi Là Số Gì