18 Bằng Bao Nhiêu – Căn Bậc Hai Của 8
Content
18 inch bằng bao nhiêu cm

Nắm được đơn vị chức năng 1 inch bằng bao nhiêu cm không riêng gì khiến cho bạn quy đổi những đơn vị đo nhanh hơn, thuận tiện khi tính toán, làm bài tập mà còn hoàn toàn có thể dễ dàng nắm được kích cỡ của màn hình hiển thị các thiết bị điện tử hiện nay. Vậy phương pháp giám sát và quy đổi giữa những đơn vị chức năng chức năng này như vậy nào?
Đơn vị 1 inch bằng bao nhiêu cm?
Chúng ta có những quy ước sau:
- inch = cm x 0,3937
- cm = inch/0.3937
Từ đó, người ta tính ra được:
- 1 inch = 2,54cm
- 1 inch = 25,4mm
- 1 inch = 0,0254m
Ngoài ra, người ta còn chuyển đổi inch sang những đơn vị khác được thống kê trong bảng sau:
| Inch | 1 |
| nm | 25.400.000 |
| µm | 25.400 |
| mm | 25,4 |
| dm | 0,254 |
| m | 0,0254 |
| km | 2,54.10-5 |
Chuyển từ đơn vị Inch sang Pixel
Pixel là một đơn vị được sử dụng khi đo độ phân giải hiển thị của những thiết bị điện tử, hoặc tranh vẽ kỹ thuật số, các ứng dụng sửa đổi ảnh (photoshop, Adobe Illustrator…). Pixel là vấn đề ảnh có kích thước được quy ước là một px = 0,26 x 0,35mm.
Với quy ước trên, tất cả chúng ta hoàn toàn có thể thấy rằng đơn vị chức năng px tương đương với các đơn vị như mét vuông, centimet vuông,… Bởi vậy nên không hề quy đổi từ Inch sang pixel được.
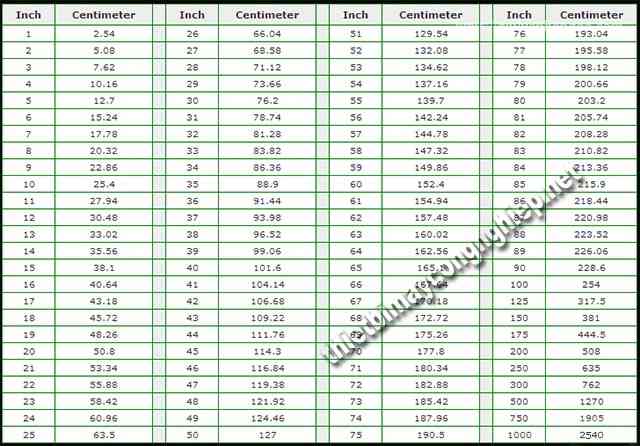
Để có thể thuận tiện hơn khi thực hiện đổi 1 inch bằng bao nhiêu cm mm bạn có thể sử dụng bảng chuyển đổi quốc tế. Bảng này là cách chuyển đổi chuẩn nhất do hội đo lường và thống kê quốc tế thực thi và lập nên. Các dữ liệu, số liệu mẫu trong bảng sẽ giúp bạn dễ dàng quy đổi từ inch sang cm và ngược lại.
Chỉ cần nhìn vào cột inch và nhìn sang cùng hàng đó bên cột cm là hoàn toàn có thể biết được kết quả chuyển đổi. Ví dụ, muốn đổi 18 inch sang cm thì bạn nhìn số 18 tại cột inch. Sau đó nhìn sang hàng của cột cm bên cạnh là 45,72 cũng sẽ nghĩa là 18 inch = 45,72cm vô cùng đơn giản.
Căn 50 bằng bảo nhiều
Phương pháp 1Phương pháp 1 của 3:Rút gọn căn bậc hai bằng cách nghiên cứu và phân tích nhân tử
- 1Hiểu phân tích nhân tử là gì. Mục tiêu của quy trình rút gọn căn bậc hai là viết lại nó dưới dạng dễ hiểu và đơn thuần hơn nhằm giải những thắc mắc toán học. Phân tích nhân tử là cách chia một số lớn hơn thành nhiều nhân tử nhỏ hơn, ví dụ tách 9 thành 3 x 3. Khi ta đã tìm ra những nhân tử của số đang xét, ta hoàn toàn hoàn toàn có thể viết lại căn bậc hai của số đó thành dạng đơn giản hơn, thậm chí có thể thành một số ít nguyên. Chẳng hạn √9 = √(3×3) = 3. Các bước sau đây sẽ chỉ cho bạn thấy tiến trình rút gọn những căn bậc hai phức tạp hơn.
- 2Lấy số dưới căn chia cho số nguyên tố nhỏ nhất có thể. Nếu phần dưới căn là số chẵn, hãy chia cho hai. Nếu đây là số lẻ thì thử xem nó có chia hết cho 3 hay không. Trong trường hợp số dưới căn không chia hết cho cả 2 và 3, hãy triển khai chia cho những số nguyên tố tiếp theo trong danh sách sau đây cho tới khi tìm kiếm được ước số nguyên tố nhỏ nhất của số dưới căn. Ta chỉ xét tới những số nguyên tố bởi tất cả những số khác đều hoàn toàn có thể nghiên cứu và phân tích thành tích của một số ít nguyên tố với nhân tử khác. Ví dụ, ta sẽ không lấy phần dưới căn chia cho 4, vì bất cứ số nào chia hết cho 4 thì cũng chia hết cho 2.
- 3Viết lại căn bậc hai theo dạng bài toán về phép nhân. Giữ toàn bộ các nhân tử dưới dấu căn. Ví dụ, khi rút gọn √98, ta thấy 98 ÷ 2 = 49, vì vậy 98 = 2 x 49. Vì thế, ta hoàn toàn có thể viết lại là: √98 = √(2 x 49).
- 4Lặp lại tiến trình trên với nhân tử còn lại. Trước khi rút gọn căn bậc hai đang xét, tất cả chúng ta cần tách nhân tử cho tới khi ta được hiệu quả phép phân tích là hai số giống hệt nhau. Nhắc lại ý nghĩa của căn bậc hai, ta sẽ thấy điều này trọn vẹn hợp lý: vì √(2 x 2) có nghĩa là “số mà khi nhân với chính nó ta sẽ tiến hành hiệu quả là 2 x 2.” Và rõ ràng trong trường hợp này đó đó chính là số 2. Tương tự, ta lặp lại các bước này với ví dụ đang xét √(2 x 49):
- Ta đã tách được nhân tử 2. (Nói cách khác, đấy là một Một trong những số nguyên tố được nêu ở list trên). Vì vậy, ta sẽ bỏ qua số này và liên tục tách 49 thành các nhân tử nhỏ hơn.
- 49 không chia hết cho 2, 3 hay 5. Ta có thể kiểm chứng bằng phương pháp sử dụng máy tính hoặc thực thi phép chia. Vì kết quả phép chia 49 cho 2, 3 hoặc 5 không cho ta 1 số ít nguyên nên ta sẽ bỏ lỡ các số này và chia tiếp.
- 49 hoàn toàn có thể chia hết cho 7. Ta có 49 ÷ 7 = 7, tức là 49 = 7 x 7.
- Viết lại bài toán, ta được: √(2 x 49) = √(2 x 7 x 7).
- 5″Rút” một số ít ra khỏi dấu căn. Khi ta đã phân tích số đang xét thành các nhân tử, trong đó có hai số giống hệt nhau, ta hoàn toàn có thể kéo số đó ra khỏi dấu căn. Tất cả những nhân tử còn sót lại không thay đổi dưới dấu căn. Ví dụ: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).
- Ta hoàn toàn có thể dừng việc phân tích khi đã tìm ra hai nhân tử giống nhau. Ví dụ √(16) = √(4 x 4) = 4. Nếu ta liên tục việc nghiên cứu và phân tích thì kết quả ở đầu cuối vẫn không thay đổi, chỉ khác là ta phải triển khai chia nhiều lần hơn: √(16) = √(4 x 4) = √(2 x 2 x 2 x 2) = √(2 x 2)√(2 x 2) = 2 x 2 = 4.
- 6Nếu số lượng nhân tử dưới căn nhiều hơn thế nữa một thì ta nhân chúng lại với nhau. Với những căn bậc hai lớn, ta hoàn toàn có thể thực thi rút gọn nhiều lần. Trong trường hợp đó, lấy tích các nhân tử sẽ cho tác dụng cuối cùng. Xét ví dụ dưới đây:
- √180 = √(2 x 90)
- √180 = √(2 x 2 x 45)
- √180 = 2√45, tuy nhiên phần căn còn sót lại vẫn đang còn thể nghiên cứu và phân tích tiếp thành nhân tử nhỏ hơn
- √180 = 2√(3 x 15)
- √180 = 2√(3 x 3 x 5)
- √180 = (2)(3√5)
- √180 = 6√5
- 7Ghi “không thể rút gọn” nếu phép phân tích nhân tử không cho hai số giống nhau. Một số căn bậc hai thực chất đã ở dạng tối giản. Nếu ta liên tục phân tích đến khi tất cả những nhân tử dưới căn là số nguyên tố (đã được nêu ở những bước trên) mà hoàn toàn không còn hai số nào giống nhau thì tức là ta không thể tối giản thêm nữa. Có thể đề bài đang xét là một bài mẹo mà thôi! Ví dụ, hãy tối giản √70:
- 70 = 35 x 2, do đó √70 = √(35 x 2)
- 35 = 7 x 5, nên √(35 x 2) = √(7 x 5 x 2)
- Cả ba số trên đều là số nguyên tố, cho nên vì thế ta không thể tối giản thêm nữa. Thêm vào đó, ba số này đều khác nhau nên ta không hề kéo một trong ba số thoát khỏi dấu căn. Vì vậy √70 không hề rút gọn được nữa.
Quảng cáo
Phương pháp 2Phương pháp 2 của 3:Số chính phương
- 1Ghi nhớ các số chính phương. Bình phương một số, hay có thể nói rằng là lấy 1 số ít nhân với chính nó, sẽ cho ta tác dụng là một số chính phương. Ví dụ, 25 là số chính phương vì 5 x 5, tức 52, bằng 25. Hãy nỗ lực ghi nhớ tối thiểu mười số chính phương tiên phong vì từ đó chúng hoàn toàn có thể giúp ta thuận tiện nhận ra căn bậc hai tương ứng. Mười số chính phương đầu tiên gồm:
- 12 = 1
- 22 = 4
- 32 = 9
- 42 = 16
- 52 = 25
- 62 = 36
- 72 = 49
- 82 = 64
- 92 = 81
- 102 = 100
- Tìm căn bậc hai của một số chính phương. Nếu thấy một số chính phương dưới dấu căn, ta có thể chuyển số đó về dạng tích của hai số giống nhau, từ đó triệt tiêu được dấu căn. Ví dụ, khi thấy phần dưới căn là 25, ta biết là giá trị của căn bậc hai này bằng 5 vì 25 là số chính phương và bằng 5 x 5. Tương tự, ta có mức giá trị căn bậc hai của những số chính phương nêu trên như sau:
- √1 = 1
- √4 = 2
- √9 = 3
- √16 = 4
- √25 = 5
- √36 = 6
- √49 = 7
- √64 = 8
- √81 = 9
- √100 = 10
- 2Phân tích nhân tử thành những số chính phương. Khi rút gọn căn bậc hai, hãy sử dụng các số chính phương trong bước nghiên cứu và phân tích nhân tử. Nếu có thể tách được một số chính phương thì việc rút gọn sẽ đỡ mất thời hạn hơn. Dưới đây là 1 số ít mẹo:
- √50 = √(25 x 2) = 5√2. Nếu hai chữ số cuối cùng của số đang xét là 25, 50 hoặc 75, ta luôn tách được số 25 thoát khỏi số đó.
- √1700 = √(100 x 17) = 10√17. Nếu hai chữ số sau cuối của số đang xét là 00, ta luôn tách được 100 ra khỏi số đó.
- √72 = √(9 x 8) = 3√8. Nhận biết được bội số của 9 cũng giúp ích thật nhiều khi nghiên cứu và phân tích nhân tử. Mẹo nhận ra bội số của 9 như sau: nếu tổng toàn bộ những chữ số của số đang xét bằng 9 hoặc chia hết cho 9 thì số đó chia hết cho 9.
- √12 = √(4 x 3) = 2√3. Không có mẹo nào để nhận biết 1 số ít có chia hết cho 4 không, tuy nhiên với những số không quá lớn, việc thực hiện phép chia cho 4 không quá phức tạp. Hãy ghi nhớ số chính phương này khi nghiên cứu và phân tích nhân tử.
- 3Phân tích 1 số ít thành tích của nhiều số chính phương. Nếu số đang xét là tích của nhiều hơn 1 số ít chính phương, ta hoàn toàn có thể đưa tổng thể ra ngoài dấu căn. Trong quá trình rút gọn căn bậc hai, nếu kết quả nghiên cứu và phân tích nhân tử có không ít số chính phương, ta rút căn bậc hai của chúng ra khỏi dấu căn và nhân lại với nhau. Ví dụ rút gọn √72:
- √72 = √(9 x 8)
- √72 = √(9 x 4 x 2)
- √72 = √(9) x √(4) x √(2)
- √72 = 3 x 2 x √2
- √72 = 6√2
Quảng cáo
Phương pháp 3Phương pháp 3 của 3:Các thuật ngữ
- 1Dấu (√) là dấu căn bậc hai. Ví dụ trong bài toán √25, thì “√” là dấu căn.
- 2Số dưới căn là số được viết dưới dấu căn. Ta cần tìm giá trị căn bậc hai của số đó. Ví dụ, với √25, “25” là số dưới căn.
- 3Hệ số căn là số nằm ngoài dấu căn. Đây đó chính là số nhân với căn bậc hai và nằm cạnh sát trái dấu căn. Ví dụ với 7√2, thì “7” là thông số căn.
- 4Kết quả của một phép chia hết được gọi là nhân tử. Ví dụ, 2 là nhân tử của 8 vì 8 ÷ 4 = 2, 3 không phải là nhân tử của 8 vì 8÷3 không cho hiệu quả là một số nguyên. Ví dụ, 5 là nhân tử của 25 vì 5 x 5 = 25.
- 5Ý nghĩa của sự việc rút gọn căn bậc hai. Rút gọn căn bậc hai chính là sự việc tách những số chính phương thoát khỏi số dưới căn, rút căn bậc hai của những số chính phương đó ra khỏi dấu căn đồng thời giữ lại phần nhân tử còn sót lại dưới dấu căn. Nếu số dưới căn là 1 số ít chính phương thì sau khi rút gọn ta sẽ triệt tiêu được dấu căn. Ví dụ, √98 hoàn toàn có thể rút gọn thành 7√2.Quảng cáo
Căn 18 bằng bao nhiêu
Hiện nay đa phần máy tính bỏ túi đều có phím căn bậc hai. Các bảng tính máy tính và ứng dụng khác cũng thường được sử dụng để tính căn bậc hai. Máy tính bỏ túi thường thực hiện những chương trình hiệu quả, như chiêu thức Newton, để tính căn bậc hai của một số ít thực dương.[3][4] Khi tính căn bậc hai bằng bảng lôgarit hay thước lôga, hoàn toàn có thể tận dụng giống hệt thức
- √a = e (ln a) / 2 hay √a = 10 (log10 a) / 2.
trong đó ln và log10 lần lượt là logarit tự nhiên và logarit thập phân.
Vận dụng phương pháp thử (thử và sai, trial-and-error) có thể ước tính √a và thêm bớt cho tới khi đủ độ đúng chuẩn cần thiết. Giờ xét một ví dụ đơn giản, để tính √6, trước tiên tìm hai số chính phương sớm nhất với số dưới dấu căn, 1 số ít lớn hơn và một số ít nhỏ hơn, đây là 4 và 9. Ta có √4 < √6 < √9 hay 2 < √6 < 3, từ đây có thể nhận thấy √6 nhỏ hơn và gần 2,5, chọn giá trị ước tính là 2,4. Có 2,42 = 5,76 < 6 < 6,25 = 2,52 suy ra 2,4 < √6 < 2,5; từ đây tiếp tục thấy rằng √6 gần với trung bình của 2,4 và 2,5, vậy giá trị ước đoán tiếp theo là 2,45…
Phương pháp lặp thông dụng nhất để tính căn bậc hai mà hoàn toàn không dùng máy tính được nghe biết với tên gọi “phương pháp Babylon hay “phương pháp Heron” theo tên người đầu tiên miêu tả nó, triết gia người Hy Lạp Heron of Alexandria.[5] Phương pháp này sử dụng sơ đồ lặp tựa như chiêu thức Newton–Raphson khi ứng dụng hàm số y = f(x)=x2 − a.[6] Thuật toán là sự tái diễn một phương pháp tính đơn thuần mà hiệu quả sẽ ngày càng gần hơn với căn bậc hai thực mỗi lần lặp lại. Nếu x ước tính lớn hơn căn bậc hai của một số thực không âm a thì a/x sẽ nhỏ hơn và bởi vậy trung bình của hai số này sẽ là giá trị chính xác hơn bản thân mỗi số. Tuy nhiên, bất đẳng thức AM-GM chỉ ra giá trị trung bình này luôn lớn hơn căn bậc hai thực, do đó nó sẽ tiến hành dùng như một giá trị ước tính mới lớn hơn đáp số thực để tái diễn quá trình. Sự quy tụ là hệ quả của việc những kết quả ước tính lớn và nhỏ hơn gần nhau hơn sau từng bước tính. Để tìm x:
- Khởi đầu với một giá trị x dương bất kỳ. Giá trị này càng gần căn bậc hai của a thì sẽ càng cần ít bước lặp lại để đạt độ đúng chuẩn mong muốn.
- Thay thế x bằng trung bình (x + a/x) / 2 của x và a/x.
- Lặp lại bước 2, sử dụng giá trị trung bình này như giá trị mới của x.
Vậy, nếu x0 là đáp số phỏng đoán của √a và xn + 1 = (xn + a/xn) / 2 thì mỗi xn sẽ giao động với √a hơn với n lớn hơn.
- √a = 2-n√4n a,
việc tính căn bậc hai của 1 số ít dương hoàn toàn có thể được đơn thuần hóa thành tính căn bậc hai của một số trong mức [1,4). Điều này giúp tìm giá trị đầu cho giải pháp lặp gần hơn với đáp số chuẩn xác.
Một phương pháp hữu dụng khác để tính căn bậc hai là thuật toán đổi khác căn bậc n, vận dụng cho n = 2.
Căn 72 bằng bao nhiêu
72 (bảy mươi hai) là số tự nhiên đứng sau 71 và đứng trước 73. Nó là 50% tổng hoặc 6 chục (tức là 60 trong hệ thập phân).
Các yếu tố của 36 có quan hệ như thế nào với những yếu tố của 72? GCF là 72 và 36 theo thừa số nguyên tố
Như hoàn toàn có thể thấy, 72 và 36 có chung những thừa số nguyên tố. Do đó, GCF của 72 và 36 là 2 × 2 × 3 × 3 = 36.
| Con số | nguyên tố | Bộ chia |
| 70 | 2 * 5 7 * | 1,2,5,7,10,14,35,70 |
| 71 | 71 | 1,71 |
| 72 | 2 3 * 3 2 | 1,2,3,6,8,9,12,24,36,72 |
| 73 | 73 | 1,73 |
Làm thế nào để bạn tìm thấy một yếu tố? Làm thế nào để tìm số yếu tố?
- Tìm thừa số nguyên tố của nó, tức là bộc lộ nó dưới dạng tích của những số nguyên tố.
- Viết thừa số nguyên tố dưới dạng số mũ.
- Thêm 1 vào mỗi số mũ.
- Nhân tổng thể những số kết quả.
- Sản phẩm này sẽ cung cấp số lượng những yếu tố của một số ít đã cho.
Làm thế nào để bạn tìm thấy yếu tố tích cực?
Để tìm số thừa số của một số đã cho, hãy biểu lộ số đó dưới dạng tích góp thừa của các số nguyên tố. Bây giờ, hãy tăng lũy thừa của mỗi số nguyên tố với cùng 1 và nhân kết quả. Do đó, sẽ có 10 thừa số gồm có 1 và 48. Nếu loại trừ, hai số này, các bạn sẽ có 10 – 2 = 8 thừa số.
Các yếu tố của 73 là gì? 73 là 1 số ít ít nguyên tố vì nó chỉ có hai yếu tố, 1 và 73.
72 chia hết cho 3 có hay không?
Vì câu vấn đáp cho phép chia của tất cả chúng ta là một số nguyên, chúng ta biết rằng 72 chia hết cho 3.
Làm thế nào để bạn hiển thị 72 chia cho 8? Sử dụng máy tính, nếu khách hàng nhập 72 chia 8, bạn sẽ nhận được 9. Bạn cũng có thể biểu lộ 72/8 dưới dạng phân số hỗn hợp: 9 0/8.
Căn bậc hai của 8
Thừa số nguyên tố của 54 là 2 × 3 × 3 × 3, do đó, căn bậc hai của 54 ở dạng căn nhỏ nhất của nó được biểu lộ bằng 3 ∛2 .
…
Gốc khối 54.
| 1. | Gốc Cube của 54 là gì? |
| 3. | Cube Root của 54 phi lý? |
| 4. | Câu hỏi thường gặp về Cube Root of 54 |
Ngoài ra 64 cube root là gì? Vì căn bậc hai của 64 là 1 số ít nguyên, nên 64 là một hình lập phương hoàn hảo.
…
Căn bậc hai của 64 ở dạng căn: ∛64.
| 1. | Gốc Cube của 64 là gì? |
| 3. | Cube Root của 64 phi lý? |
| 4. | Câu hỏi thường gặp về Cube Root of 64 |
Khối lập phương của 5 là gì?
Căn bậc hai của 5 được biểu lộ bằng ∛5 ở dạng căn và dưới dạng (5) ⅓ hoặc (5) 0 . 33 ở dạng số mũ.
…
Căn bậc hai của 5 ở dạng Cơ số: ∛5.
| 1. | Gốc Cube của 5 là gì? |
| 3. | Cube Root của 5 phi lý? |
| 4. | Câu hỏi thường gặp về Cube Root of 5 |
Khối lập phương từ một đến 10 là gì? Các số lập phương từ 1 đến 100
| Con số | Cube |
| 8 | 512 |
| 9 | 729 |
| 10 | 1000 |
| 11 | 1331 |
• Ngày 4 tháng 2020 năm XNUMX
Blog -10 8 Dương Là Bao Nhiêu Âm – 10 Tháng 9 Dương Là Ngày Bao Nhiêu Âm
1 Quart Bằng Bao Nhiêu Lít – Quartz Là Gì
1 Cc Bằng Bao Nhiêu Giọt – 1 Giọt Nước Bao Nhiêu Gram
1 Bát Cháo Lòng Bao Nhiêu Calo – Cháo Lòng Bao Nhiêu Tiền
1 Bao Bột Trét Được Bao Nhiêu M2 – Các Loại Bột Trét Tường
Đậu Rồng Bao Nhiêu Calo – 100G Đậu Rồng Bao Nhiều Protein
Yến Vụn Giá Bao Nhiêu – Mua Yến Vụn Ở Đâu